Matched Filter Technique (MFT)
The recently developed MFT is revealed to be a power tool to help identify missing events [Peng and Zhao, 2009] with small signal to noise ratio, which could happen when earthquakes occurred very frequently (earthquake swarm) or masked by large amplitude surface/coda wave following large mainshock. The physics behind this technique is earthquakes spatially close would have similar waveform recorded by the same station. Using events listed in standard earthquake catalog as template to scan through continuous waveform, missing events around the templates would be able to be identified.
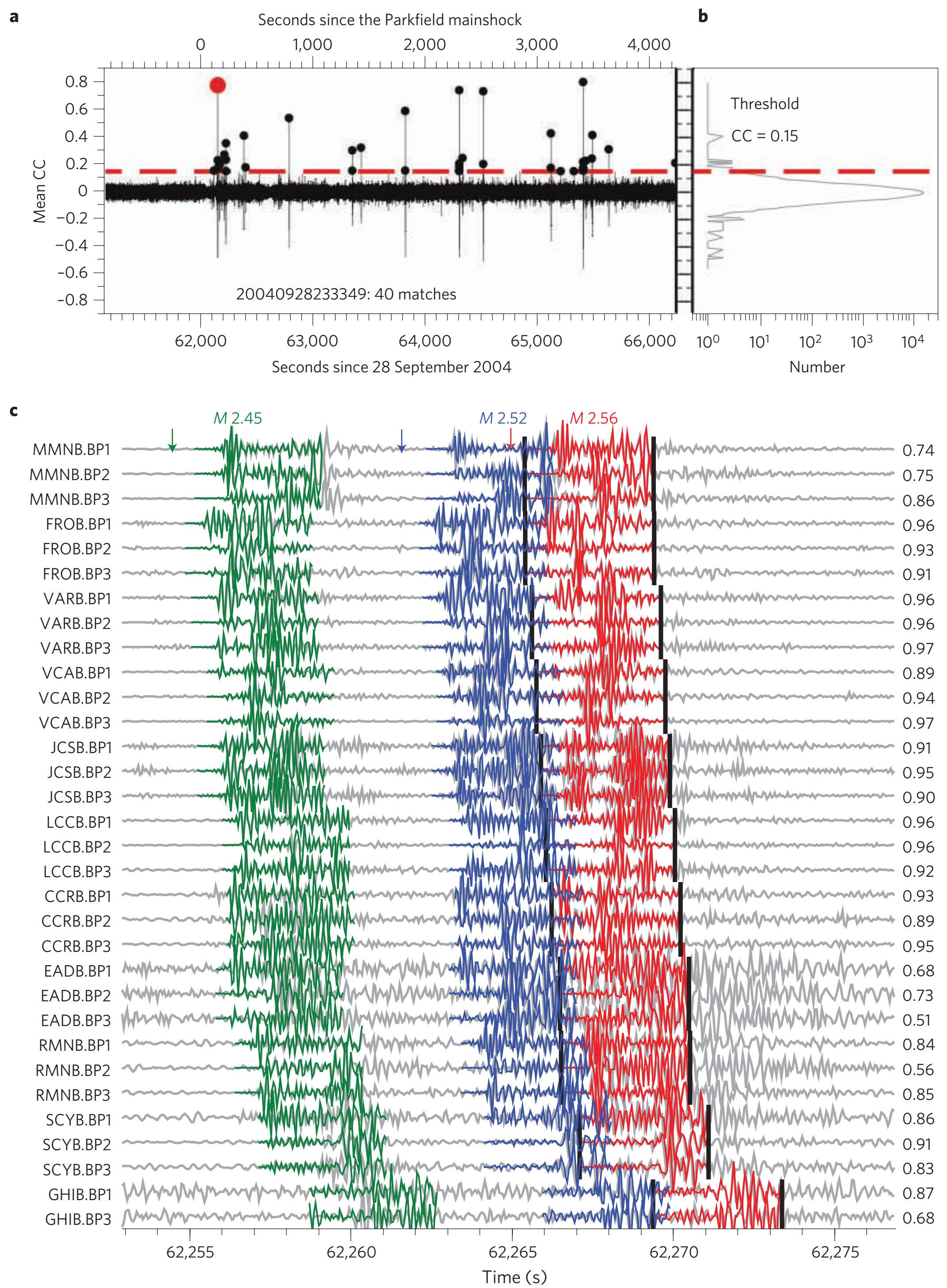
The work flow contains: prepare the continuous waveform (pre-processing, shift origin time, band-pass filter waveform); process the templates (use catalog to cut template waveform, compute the signal to noise ratio); operate channel-wise sliding-window cross-correlation as well as stacking; clean up the final catalog. If you are interested, you can take a look of the tutorial ppt [MFT_PDF].
Dr. Xiaofeng Meng has a nice online website tutorial about MFT. Please find the following link: Meng's Tutorial.
HypoDD Relocation
1. Overview of hypoDD package
HypoDD is a Fortan program package for relocating earthquakes with the double-difference (DD) algorithm of Waldhauser and Ellsworth (2000).
The DD technique takes advantage of the fact that if the hypocentral separation between two earthquakes is relatively small compared to the event-station distance and the scale length of velocity heterogeneity, then the ray paths between the souce region and a common station are similar along almost the entire ray path, and the difference in travel times for two events observed at one station can be attributed to the spatial offset between the events with high accurracy.
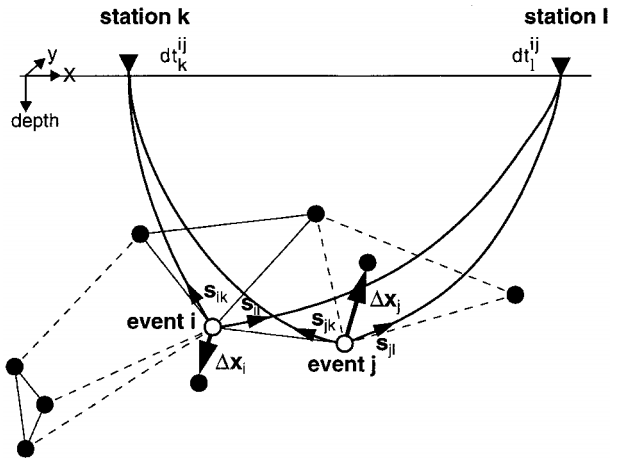
Theoretical travel times are calculated for current hypocenters at stations where the phase was recorded. The DD residuals for pairs of earthquakes at each station are minimized by weighted least squares using the method of SVD or LSQR. Solutions are found by iteratively adjusting the vector difference between the nearby pairs, with the locations and partial derivatives being updated after each iteration.
Earthquake relocation with hypoDD is a two-step process. The fist step involves the analysis of catalog phase data and/or waveform data to derive travel time differences for pairs of earthquakes, which is necessary to optimize the linkage between events and minimize redundancy in the dataset. In the second step, the differential travel time from step one is used to determine DD hypocenter locations. It solves for hypocentral separation after insuring thta the network of vectors connecting each earthquake to its neighbors has no weak link that would lead to numerical instabilities.
2. Source Code and User Guide
Freely download the most recent version HypoDD v1.3. Unzip the file and go to each directory which contains the source code and compile the code. Then add the paths to your .bashrc in order to use them.
Acess to the User Guide for using both ph2dt and hypoDD programs. ph2dt transforms phase data into catalog differential time input for hypoDD, and hypoDD performs the DD relocations.
3. Two Programs: ph2dt & hypoDD
ph2dt searches catalog P and S phase data for event pairs with travel time information at common stations to optimize the quality of phase pairs and event connectivity. Ideally, it attempts to build a network of links between events so that there exists a chain of pairwise connected events from one event to any other event, with the distance being as small as possible between connected events.
ph2dt establishes such a network by building links from each event to a maximum of MAXNGH neighboring events within a search radius defined by MAXSEP. To reach the maximum number of neighbors, only "strong" neighbors with more than MINLNK phase pairs are considered, while "weak" are not counted. The nearest neighbor approach is used to find neighboring events. To avoid very large DD observations, we can restrict the number of links for each event pair by defining a mimimum (MINOBS) and a maximum (MAXOBS) number of observations to be selected for each event pair.
ph2dt removes observations that are considered as outliers, which are identified as delay times are larger than the maximum expected delay time for a given event pair. After linking together all events, value of the average distance between strongly linked events indicates the density of the hypocenter distribution and would guide on the choice of the maximum hypocenter separation allowed in hypoDD (WDCT).
The grouping of events into clusters of well-connected events is explicitly performed in hypoDD to ensure stability of the inversion. To improve connectedness throughout a cluster of events, the values of MAXNGH and/or MINLNK can be increased in ph2dt to reach more distant neighbors for each event at the cost of introducing model errors during relocation.
Waveform based differential arrival time can be obtained from various existing techniques. Such data can be easily combined with catalog data in hypoDD. Note, however, that when using cross-correlation differential times, phases may correlate under specific event-pair station configurations only, such as in cases where the event pair is small compared to the distance to a common station and focal mechanism are very similar. Thus, although the measurements may be of high accuracy, the spread of the partial derivatives might not be optiaml to control the relative locations of the two events.
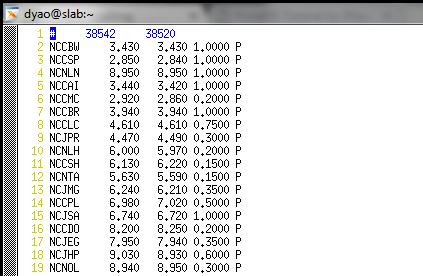
Screenshots for necessary files ph2dt.inp phase.dat can be found below.
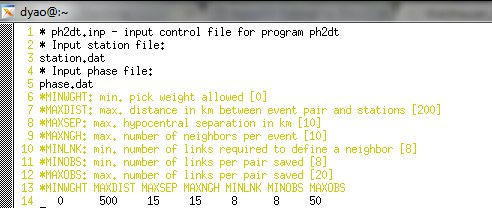
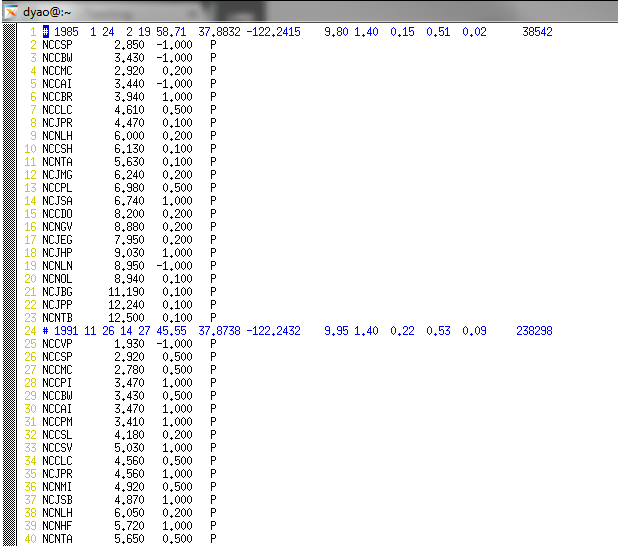
Important Notes: 1) Every earthquake must have a unique id number. 2) Both measurements are referenced to the same event origin times if combining both catalog and waveform based travel time measuremnts.
hypoDD can process any combination of catalog and cross-correlation data. Relocating events using each data type independently is useful to assess the consistency of and the relative quality between the data types. It ensures connectedness between events by grouping events into clusters, with each cluster having a chain of links from any event to any other event in the cluster. The strength of this chain is defined by a minimum of observations (OBSCC and OBSCT) per event pair that build up the chain. Note that if the value for OBSCT is larger than the value chosen for MAXOBS in ph2dt, hypoDD will find no clusters. The value for OBSCT should generally be equal to or less than MINLNK to ensure strong links.
Another factor that controls connectivity between events is the maximum hypocentral separation allowed between linked events, which are parameters WDCT and WDCC. hypoDD removes data for event pairs with separation distances larger than the values given for WDCT and WDCC for the first iteration. Note the distance cutoff parameter WDCT is similar to the parameter MAXSEP in ph2dt. It is advised to choose a larger value for MAXSEP, and then experiment with smaller values for WDCT to keep separation distances small and still connect all events.
hypoDD minimizes residuals between observed and calculated travel time differences in a iterative procedure. Initial locations are taken from the catalog, either at reported locations or at common location at the centroid of the cluster (ISTART). ISOLV allows the choice of two methods to solve the system of DD equations: singular value decomposition SVD and the conjugate gradient method LSQR. SVD is useful for examing the behavior of small systems, while LSQR takes advantage of the sparseness of the DD equation system and is able to solve a large system efficiently.
LSQR solves the damped least squares problems. DAMP is the damping factor that damps the hypocentral adjustments if the adjustment vector becomes large or unstable. The condition of the system is expressed by the condition number (CND). Generally a damping between 1 and 100 is appropriate, resulting in a condition number that is between about 40 and 80. You can adjust the DAMP to obtain a reasonable CND: if the CND is higher (lower) DAMP needs to be increased (decreased).
The straightforward way to improve the stability of the inversion is by better constraining the solution: requiring more links between events through OBSCT/OBSCC and/or mofifying the weighting and re-weighting scheme. It might also be necessary to go back and generate a differential time data set that allows for more neighbors for each event (increasing MAXNGH or MINLNK).
The damping of the solution vector allows some control of how fast a solution converges, which effects the choice of the number of iterations (NITER). In general, the first few iterations contribute to the most of the shifts in hypocenter locations. Iteration can be stopped when the shifts in hypocenter adjustments or the RMS residual dropped below the noise level. Events would get deleted if they completely lose linkage. Also, some events would become airquakes when event pairs locate near the surface and the control in vertical offset is poor.
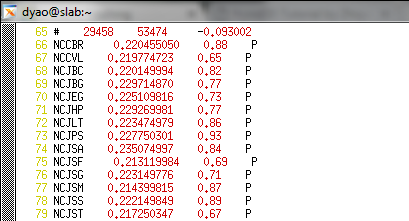
Screenshots for input files for hypoDD, which includes dt.ct (from ph2dt) and dt.cc.
4. Play with Examples
Let's start with small and medium size examples in the hypoDD program, which can be downloaded from Simple/Medium Examples. There are also three Large example datasets
Then we test with two examples to show how we apply hypoDD from scratch, and learn how to prepare the input by performing event cross correlation. Download the Waveform_Cross_Correlation Package to learn how to prepare for such data.
Perfrom waveform cross-correlation to obtain dt.cc, which can be further combined with catalog differential time.
